Kohonen Self-Organizing Maps
Self-Organizing Map is a type of ANN. And it is trained using unsupervised learning
It is used to transform an incoming signal pattern of arbitrary dimension into a one or two-dimensional discrete map
It is used for clustering data
The Architecture of Kohonen Self-Organizing Map(KSOM):
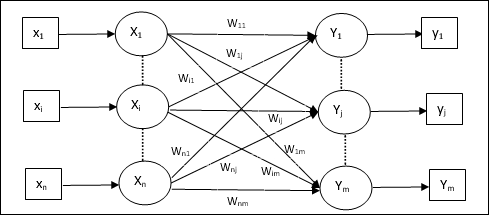
Read more about KSOM at:- https://www.tutorialspoint.com/artificial_neural_network/artificial_neural_network_kohonen_selforganizing_feature_maps.htm
Algorithm for training
Step 1 - Initialize the weights, and the learning rate η.
Step 2 - Continue steps 3-9, when the stopping condition is not true.
Step 3 - Continue steps 4-6 for every input vector x.
Step 4 - Calculate the square of Euclidean Distance for j = 1 to m.

Step 5 - Obtain the winning unit J where D(j) is the minimum.
Step 6 - Calculate the new weight of the winning unit by the following relation.

Step 7 - Update the learning rate η by the following relation -

Step 8 - Reduce the radius of the topological scheme.
Step 9 - Check for the stopping condition of the network.
I have also hard-coded the KSOFM algorithm with Python for user input:-
note - Any suggestions to make the code better will be appreciated, please share the suggestions on my email - omkoli3114@gmail.com
For learning more about KSOFM please watch videos on youtube and subscribe to my news letter.
# Declaring Initial variables
input_vector = []
intial_lrate = 0.5
weights = [[0.2, 0.4, 0.6, 0.8], [0.9, 0.7, 0.5, 0.3]]
#taking Input vector for user
for i in range(4):
x = int(input("Enter your input vectors:"))
input_vector.append(x)
print("Input Vector: ", input_vector)
print("Intial Weights: ", weights)
# creating variable for storing calculated euclidean dist
calculated_dist = []
for i in range(2):
temp = []
total = 0
weight = weights[i]
def euclidean_dist(input_vector, weight):
tryi = 0
sq_dif = (input_vector - weight)*(input_vector - weight)
temp.append(sq_dif)
for a in range(4):
euclidean_dist(input_vector[a], weight[a])
for x in temp:
total = total + x
calculated_dist.append(total)
print(calculated_dist)
#calculating winning cluster and updating the weights
update_weights = []
def Update_winning_cluster(input_vec, w):
w_new = w + intial_lrate*(input_vec - w)
update_weights.append(w_new)
#finding the lowest euclidean distance
if calculated_dist[0]<calculated_dist[1]:
print("Lowest Dist: ", calculated_dist[0])
winning_weights = weights[0]
for b in range(4):
Update_winning_cluster(input_vector[b], winning_weights[b])
weights[0] = update_weights
else:
print("Lowest Dist: ", calculated_dist[1])
winning_weights = weights[1]
for b in range(4):
Update_winning_cluster(input_vector[b], winning_weights[b])
weights[1] = update_weights
#printing the updated weights
print("updated weights are : ",weights)
